허프 변환 hough transform
Updated:
Tags: computer_vision
개요
허프 변환은 직선 탐색 알고리즘에 사용되는 변환이다.
본론
허프 변환을 설명하는 많은 문서들은 이렇게 시작한다.
허프 변환은 \(y = mx + c\) 인 직선의 방정식을 \(r = x \cos \theta + y \sin \theta\) 로 표현해서…
여기서부터 시작해보자.
여기서 우리가 나타낼 직선 \(l\) 위의 임의의 한 점을 \(P(x, y)\)라 하고,
중심이 원점이고 반지름이 \(r\)인 원을 생각해보자.
이 원은 \(\cos^2 \theta + \sin^2 \theta = r^2\) 로 나타낼 수 있고,
원의 크기를 점점 늘려간다면, 어느순간 우리의 직선 \(l\)과 만나는 접점이 생길 것이다.
이 접점을 \(T(r\cos\theta, r\sin\theta)\) 라 하자.
우리의 직선 \(l\)은 원과 접하므로 \(\overrightarrow{OT}\) 는 \(\overrightarrow{TP}\) 와 수직일 것이다. 즉, \ \(\begin{aligned} \overrightarrow{OT} \cdot \overrightarrow{TP} &= 0\\ \overrightarrow{OT} \cdot (\overrightarrow{OP} - \overrightarrow{OT}) &= 0\\ T(r\cos\theta, r\sin\theta) \cdot (P(x, y) - T(r\cos\theta, r\sin\theta)) &= 0\\ (r\cos\theta, r\sin\theta) \cdot (x-r\cos\theta, y-r\sin\theta) &= 0\\ r\cos\theta(x-r\cos\theta) + r\sin\theta(y-r\sin\theta) &= 0\\ x\cos\theta - r\cos^2\theta + y\sin\theta - r\sin^2\theta &= 0\\ x\cos\theta + y\sin\theta - r(sin^2\theta + \cos^2\theta) &= 0\\ x\cos\theta + y\sin\theta &= r \end{aligned}\\ \begin{aligned} \therefore \;\;& y=mx+c \\ & \longleftrightarrow x\cos\theta + y\sin\theta = r \end{aligned}\)
이제 \(x, y\)는 직선 위의 점에 해당하는 변수, \(r, \theta\)는 직선의 성질을 나타내는 상수라는게 느껴질 것이다.
혹은, 기울기인 \(m\)에 해당하는 개념은 \(\theta\)에 해당하고, 절편에 해당하는 \(c\)는 \(r\)에 해당한다는 인상을 받을 수 있다.
그렇다면 한 직선 위의 무수히 많은 점를 나타내는 대신, 반대로 한 점을 지나는 무수히 많은 직선을 나타내려면 어떻게 해야할까?
직선 위의 점에 해당하는 부분을 상수로 두고, 직선의 성질을 나타내는 부분을 변수로 하여 움직이면 된다.
이는 \(y=mx+c\)의 경우와 다르지 않은데, 예를 들어 직선 \(y=2x+1\)와 이를 지나는 \((1, 3)\)를 생각해보자.
식 \(y=2x+1\) 를 만족하는 여러 점 대신,
\(1=3m+c\)
를 만족하는 여러 \(m, c\) 들은 모두 \((1, 3)\)을 지난다.
\(x\cos\theta + y\sin\theta = r\) 의 경우도 마찬가지인데, \((1, 1)\)을 지나는 여러 \(\theta, r\)을 생각해보자.
가령 \(\theta = \frac{\pi}{4}, r = \sqrt{2}\), 혹은 \(\theta = 0, r = 1\)등, 다양한 직선들을 생각해볼 수 있다.
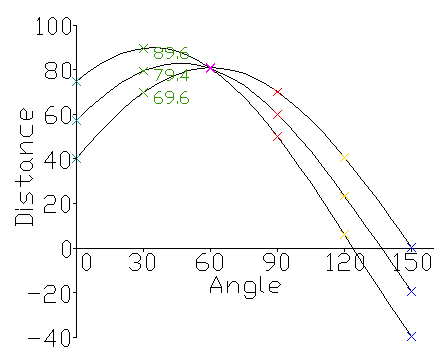
이러한 \(\theta, r\)들을 \(\theta, r\)를 축으로 하는 평면(허프만 공간)에 점을 찍으면 고유한 곡선이 나타난다.
(허프만 공간의 각 점들은 모두 고유한 직선을 나타낸다.)
따라서 직선을 구성할 것으로 의심되는 각 점을 허프만 공간으로 변환한 후, 곡선들의 교점을 찾아 다시 변환하면 직선을 찾을 수 있는데, 이는 곧 공통의 직선을 찾는 문제에서 곡선의 교점을 찾는 문제로 변환되었음을 의미한다.
예시

wikimedia commons
Leave a comment