Updated:

Categories: ,

Tags: , , , , , ,

boj 4225 쓰레기 슈트 풀이

문제

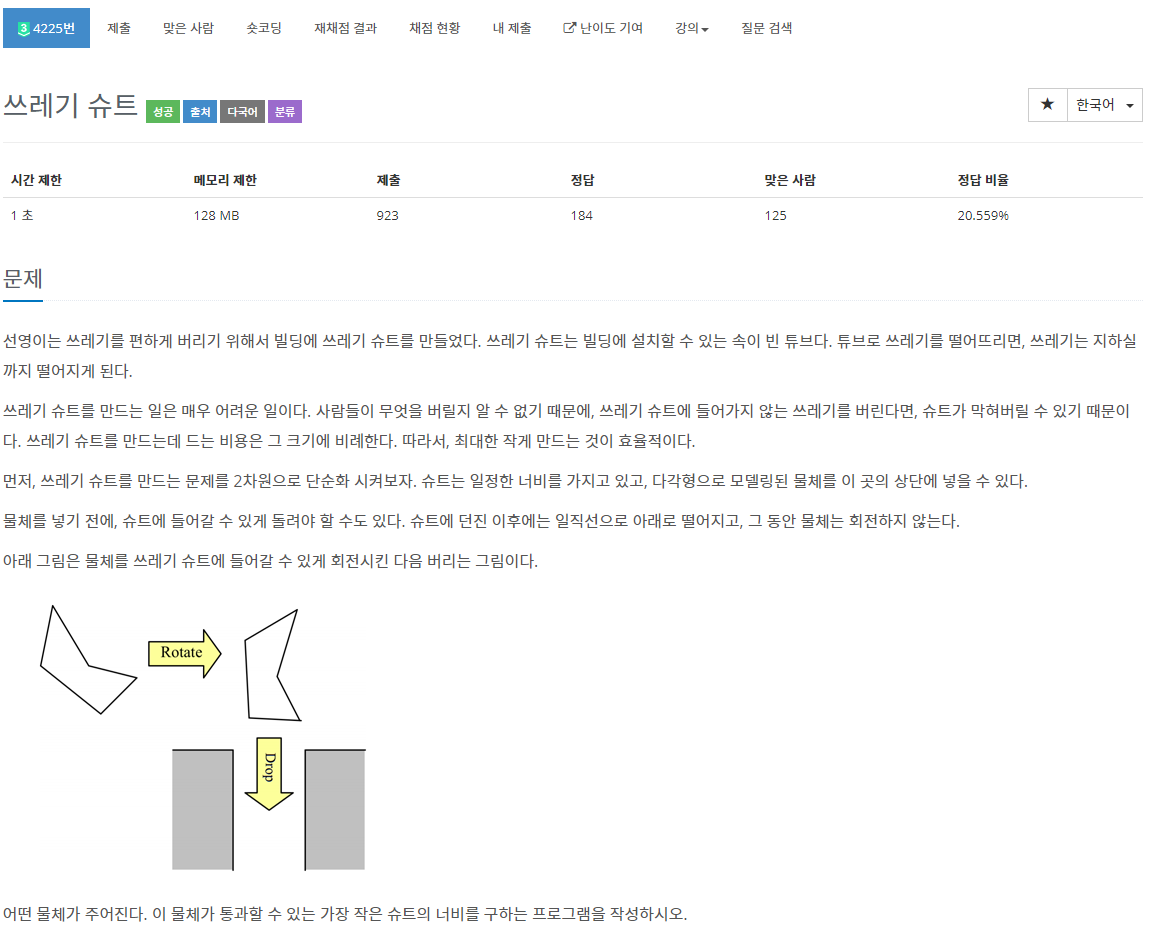
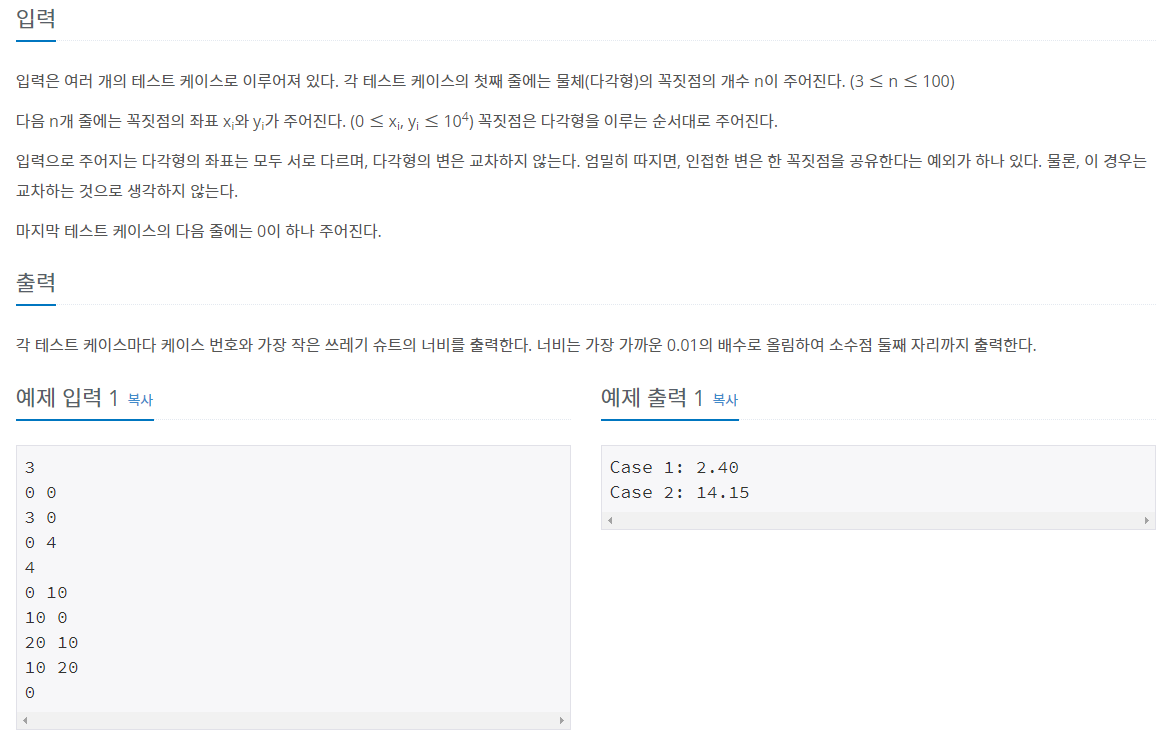
풀이

💡 쓰레기 슈트의 최소 너비는 도형의 볼록 면을 이은 선분과 다른 한 점과의 거리가 최대인 것들 중 최소이다.
즉, 볼록 면을 이은 선분이 한 쪽 벽과 맞닿아서 내려간다.

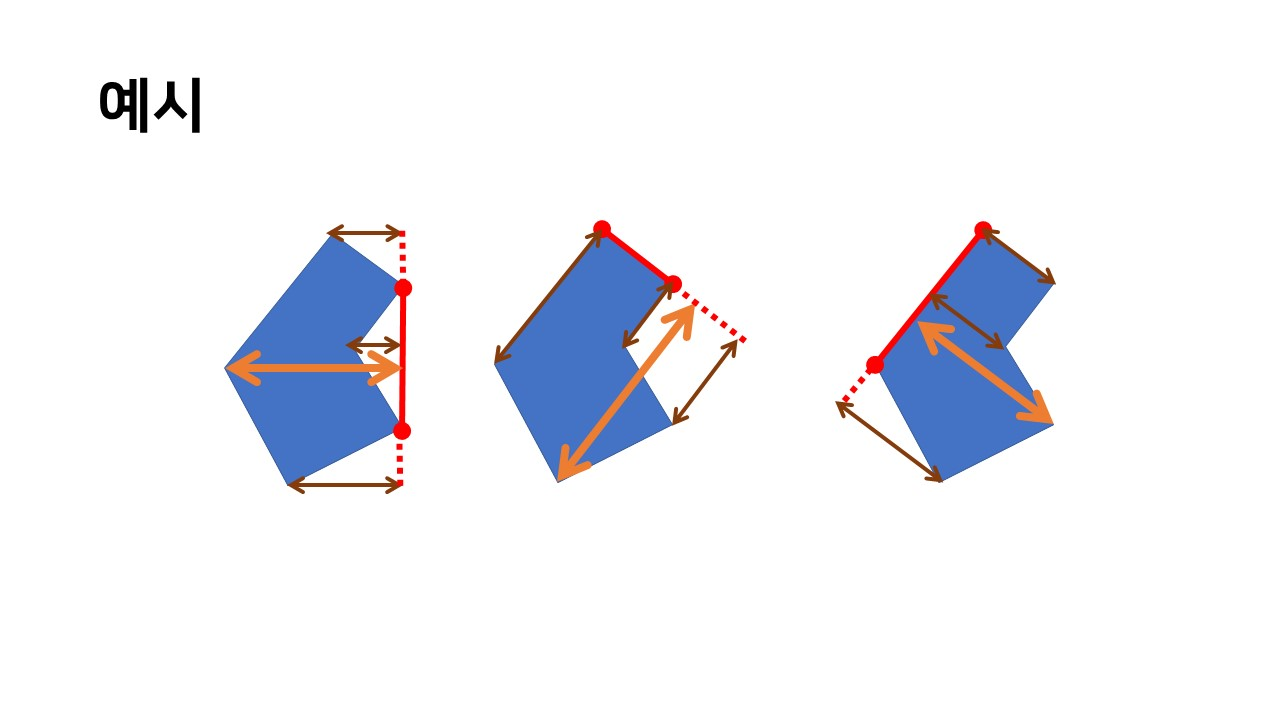
다시말해, 각 도형의 갈색 선분들 중 최대인 주황색의 선분들 중, 가장 최소인 선분이 우리가 찾는 최소 너비이다.

통로 각 병에 한 쪽 점만 닿아서 내려가는 경우가 최소 너비가 될 수 있을까?

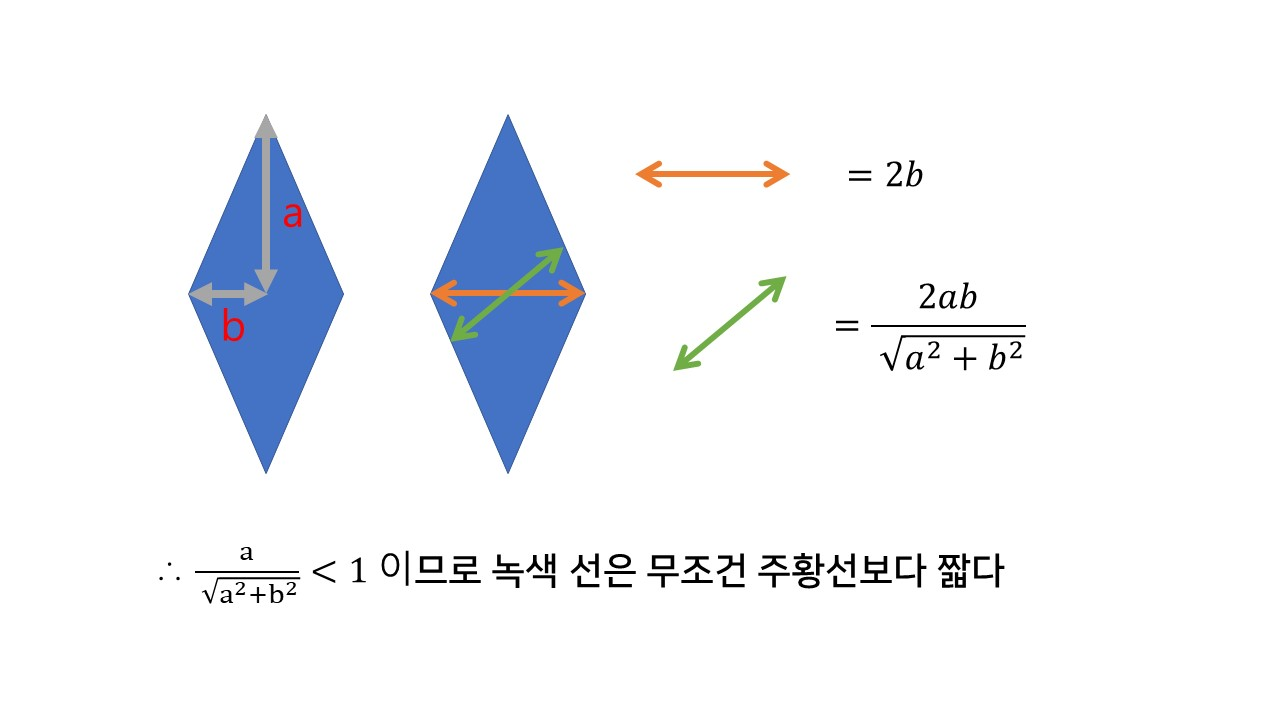
그런거 없다

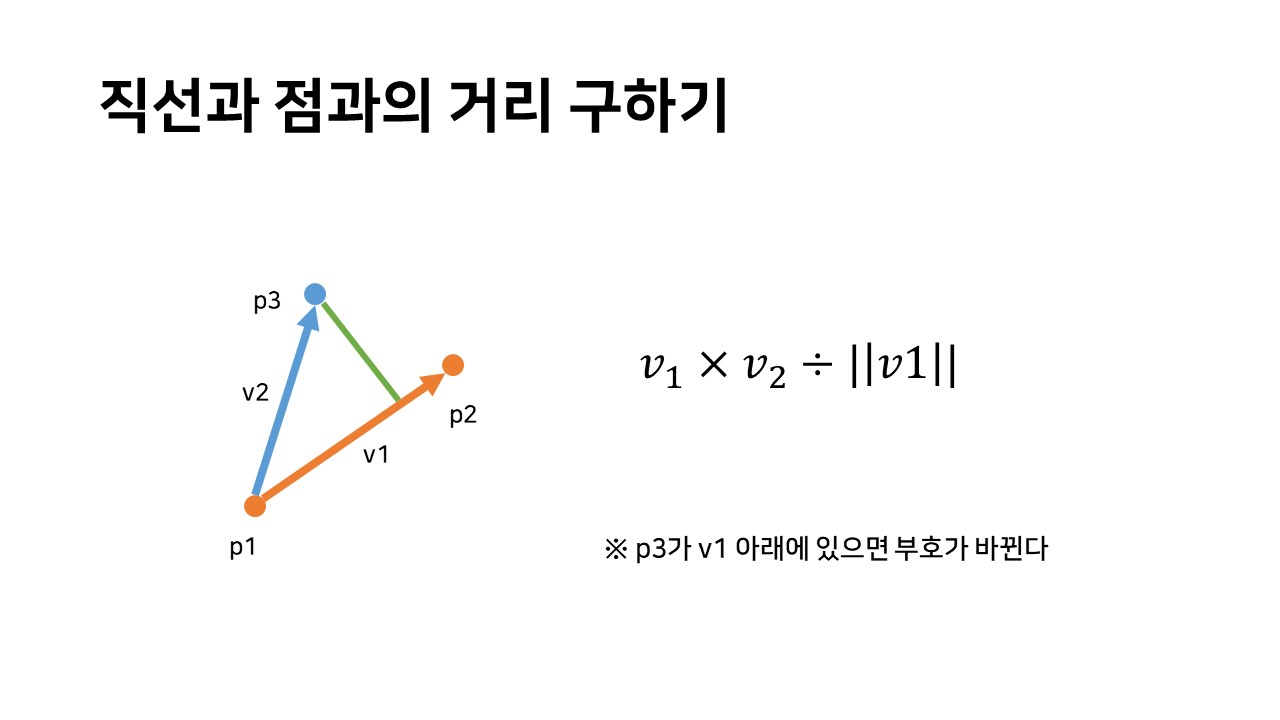
점과 직선사이의 거리는 이렇게 구할 수 있다.

최종적인 풀이는 위와 같다

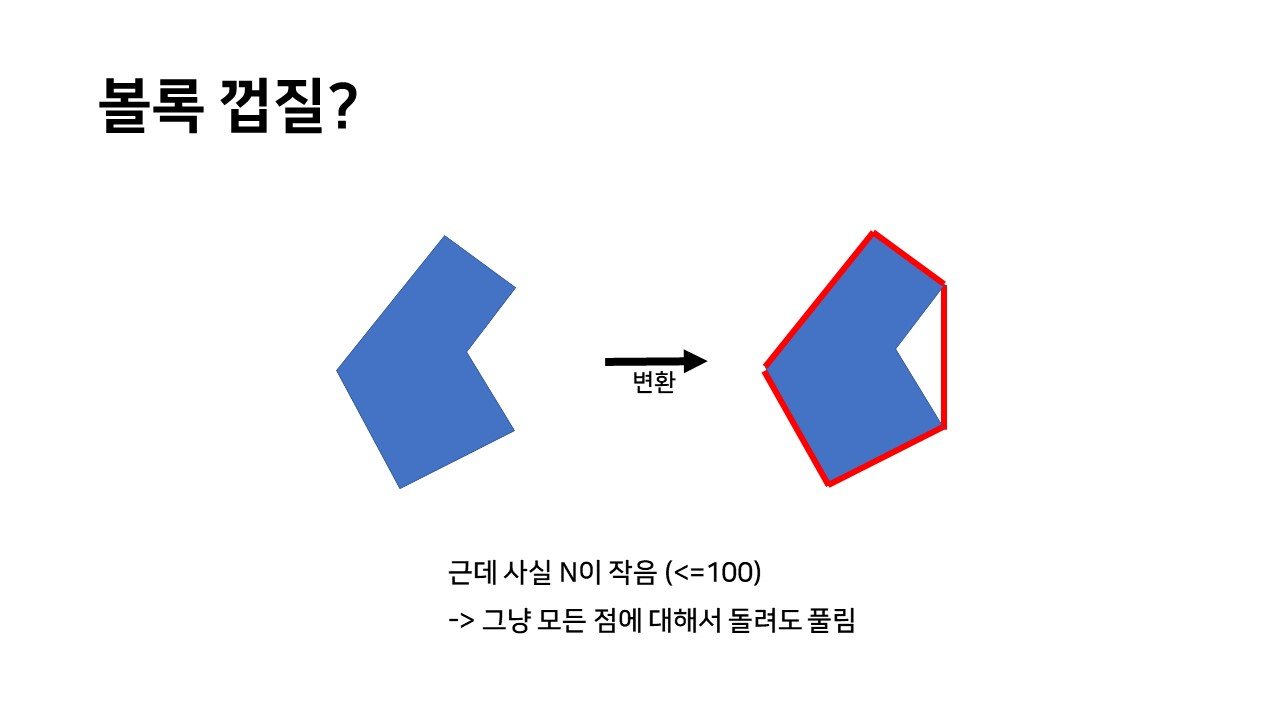
\[nC_2 \times n = \frac{n\times(n-1)}{2}\times n = O(n^3) \sim 100^3 = 1,000,000\]

근데 사실 N이 작아서 볼록 껍질(컨벡스 헐)을 따지 않아도 잘 풀리는데, 계산해보면 약 100만회의 계산이 이루어지므로, 1초의 시간제한을 고려하면 여유롭다.

만약 컨벡스헐을 통한 전처리가 이루어진다면 \(O(n^2)\)의 시간복잡도를 가진다.

코드 - w/o convex hull

C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

#include <math.h>
#include <stdio.h>
#define min(x, y) (x) < (y) ? (x) : (y)
#define max(x, y) (x) > (y) ? (x) : (y)
// 4225 쓰레기 슈트

int pts[102][2];
double dist(int p1x, int p1y, int p2x, int p2y, int p3x, int p3y) {
    return ((p3y - p1y) * (p2x - p1x) - (p3x - p1x) * (p2y - p1y))
            /hypot(p1x - p2x, p1y - p2y);
}
int main(void) {
    int tc = 0;
    while (1) {
        int n;
        double ans = 10e16;
        scanf("%d", &n);
        if (!n)
            break;
        for (int i = 0; i < n; i++) {
            int a, b;
            scanf("%d %d", &a, &b);
            pts[i][0] = a;
            pts[i][1] = b;
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < i + 1; j++) {
                double tMin = 0, tMax = 0;
                for (int k = 0; k < n; k++) {
                    double v = dist(pts[i][0], pts[i][1], pts[j][0], 
                                    pts[j][1], pts[k][0], pts[k][1]);
                    tMax = max(tMax, v);
                    tMin = min(tMin, v);
                }
                ans = min(ans, tMax - tMin);
            }
        }
        printf("Case %d: %.2f\n", ++tc, ans + 0.005);
    }
}

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include <bits/stdc++.h>
using namespace std;
// 4225 쓰레기 슈트
// https://www.acmicpc.net/problem/4225
#define X first
#define Y second
using pii = pair<int, int>;

pii pts[102];
double dist(pii &a, pii &b, pii &c) {
  return ((c.Y - a.Y) * (b.X - a.X) - (c.X - a.X) * (b.Y - a.Y)) / hypot(a.X - b.X, a.Y - b.Y);
}
int main(void) {
  ios::sync_with_stdio(0);
  cin.tie(0);

  int tc = 0;
  while (1) {
    int n;
    double ans = 10e16;
    cin >> n;
    if (!n) break;
    for (int i = 0; i < n; i++) {
      int a, b;
      cin >> a >> b;
      pts[i] = {a, b};
    }
    for (int i = 0; i < n; i++) {
      for (int j = i + 1; j < n; j++) {
        double tMin = 0, tMax = 0;
        for (int k = 0; k < n; k++) {
          double v = dist(pts[i], pts[j], pts[k]);
          tMax = max(tMax, v);
          tMin = min(tMin, v);
          if (ans < (tMax - tMin)) break;
        }
        ans = min(ans, tMax - tMin);
      }
    }
    cout << fixed;
    cout.precision(2);
    cout << "Case " << ++tc << ": " << ans + 0.005 - 1e-12 << '\n';
  }
}

python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 4225 쓰레기 슈트
from math import *
input = __import__('sys').stdin.readline

def dist(p1x, p1y, p2x, p2y, p3x, p3y):
    return ((p3y-p1y)*(p2x-p1x) - (p3x-p1x)*(p2y-p1y)) / hypot(p1x-p2x, p1y-p2y)

tc = 0
while(1):
    tc += 1
    ans = int(10**9)
    n = int(input())
    if not n: break
    pts = [list(map(int, input().split())) for _ in range(n)]

    for i in range(n):
        for j in range(i+1, n):
            tMin, tMax = 0, 0
            for k in range(n):
                v = dist(*pts[i], *pts[j], *pts[k])
                tMax = max(tMax, v)
                tMin = min(tMin, v)
                if ans < (tMax-tMin): break
            ans = min(ans, tMax-tMin)
    print('Case %d: %.2f' %(tc, ans+0.005-1e-16))

코드 - w/ convex hull

C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define min(x, y) (x) < (y) ? (x) : (y)
#define max(x, y) (x) > (y) ? (x) : (y)
// 4225 쓰레기 슈트 [CvH]
typedef long long ll;
typedef struct Point {
  int x, y;
} Pt;
int ptN, stkIdx;
Pt pts[102];
Pt stk[102];
ll ccw(Pt p1, Pt p2, Pt p3) {
  return 1ll * (p2.x - p1.x) * (p3.y - p1.y) -
         1ll * (p2.y - p1.y) * (p3.x - p1.x);
}
double perpDist(Pt p1, Pt p2, Pt p3) {
  return ccw(p1, p2, p3) / hypot(p1.x - p2.x, p1.y - p2.y);
}
int cmp1(const void *a, const void *b) {
  Pt v1 = *(Pt *)a;
  Pt v2 = *(Pt *)b;
  if (v1.x == v2.x)
    return v1.y - v2.y;
  return v1.x - v2.x;
}
int cmp2(const void *a, const void *b) {
  Pt v1 = *(Pt *)a;
  Pt v2 = *(Pt *)b;
  ll cc = ccw(pts[0], v1, v2);
  if (cc) {
    if (0 < cc)
      return -1;
    return 1;
  }
  if (v1.x - v2.x)
    return (v1.x - v2.x);
  return (v1.y - v2.y);
}
int main(void) {
  int tc = 0;
  while (1) {
    scanf("%d", &ptN);
    if (!ptN)
      break;
    double ans = 10e16;
    int a, b;
    for (int i = 0; i < ptN; i++) {
      scanf("%d %d", &a, &b);
      pts[i].x = a;
      pts[i].y = b;
    }
    qsort(pts, ptN, sizeof(Pt), cmp1);
    qsort(pts + 1, ptN - 1, sizeof(Pt), cmp2);
    stk[0] = pts[0];
    stk[1] = pts[1];
    stkIdx = 1;
    for (int idx = 2; idx < ptN; idx++) {
      Pt pp = pts[idx];
      while (1 <= stkIdx && ccw(stk[stkIdx - 1], stk[stkIdx], pp) <= 0) {
        stkIdx--;
      }
      stk[++stkIdx] = pp;
    }
    stk[++stkIdx] = stk[0];
    for (int i = 0; i < stkIdx; i++) {
      double tmp = 0;
      for (int k = 0; k < stkIdx; k++) {
        if (k == i || k == i + 1)
          continue;
        double v = perpDist(stk[i], stk[i + 1], stk[k]);
        tmp = max(v, tmp);
        if (ans < tmp)
          break;
      }
      ans = min(ans, tmp);
    }
    printf("Case %d: %.2f\n", ++tc, ans + 0.005);
  }
}

Leave a comment

You may also enjoy